上期是MPN的入門(mén)篇，相信您已經(jīng)領(lǐng)悟了MPN的意義。本期是進(jìn)階篇，主要告知MPN的數學(xué)原理，就是MPN值是怎么算出來(lái)的，可能有點(diǎn)枯燥，但是也很有趣。閱讀進(jìn)階篇需具備以下數學(xué)基礎：高中的排列組合、大學(xué)的概率論與數理統計，以及微積分。

進(jìn)階篇

入門(mén)篇里我們提到了二項式分布，從圖上看，很多人估計都會(huì )覺(jué)得這像正態(tài)分布。沒(méi)錯，僅僅也就是像而已。

我們先來(lái)搞明白這幾個(gè)隨機變量分布。二項式分布是一個(gè)比較簡(jiǎn)單的分布，適用于樣品量不大的試驗。如果把樣品量放大，概率變小，那么二項式分布就無(wú)限逼近泊松分布了。泊松分布是有限個(gè)數世界里的王者。如果把泊松分布樣品量也無(wú)限大，它就會(huì )逼近正態(tài)分布，而正態(tài)分布是無(wú)限世界的分布。有限個(gè)數和無(wú)限個(gè)數，是我自己給出的概念，目的是讓你理解。數學(xué)上叫離散型和連續型。

如果把全球70億人作為樣本，分析某個(gè)指標，你覺(jué)得應該用什么分布？只能是泊松分布，因為70億雖然很多，但是是有限個(gè)數。數學(xué)就是這么殘酷，70億很大么？毛毛雨啦。

如果想分析數字0到數字1之間的某個(gè)隨機變量的分布，那才能用到正態(tài)分布。因為0到1之間是連續的，是可以無(wú)限劃分的，只要小數點(diǎn)后面位數足夠，它就是無(wú)限的?，F在你明白，有限和無(wú)限的區別了吧。

所以我們做微生物數量分析，雖然微生物數量動(dòng)輒幾十億，上百億，但是在數學(xué)面前都是有限的。所以下面的計算只用到了泊松分布和二項式分布。

言歸正傳，MPN法是有兩個(gè)假設前提的。為了方便理解，我們還是以水質(zhì)中大腸檢驗為例。第一，大腸菌在水體中都是以均勻分散狀態(tài)存在的，沒(méi)有若干個(gè)大腸菌結成一團的情況（知道為啥樣品要均質(zhì)了吧）。第二，如果水體和水樣的容積分別以V和v表示，水體和水樣中的大腸菌數分別以n和x表示。那么，V與v相比，n與x相比，都是很大的數字。就是說(shuō)，v和x相對來(lái)說(shuō)都是小到可以忽略的數字。就好像你去長(cháng)江里取一瓶水，這瓶水對長(cháng)江來(lái)說(shuō)，可以忽略。

在容積為v的水樣中恰好出現x個(gè)大腸菌的概率符合泊松分布：

其中，x=0，1，2，3，......

在水樣容積v中恰好出現零個(gè)大腸菌的概率為：

如果每毫升水樣中的大腸菌個(gè)數為λ（注意：由此可知λ的單位是個(gè)/mL），則水樣v毫升中不出現大腸菌的概率為：

如果每毫升水樣中大腸菌個(gè)數為λ，則水樣中出現大腸菌的概率為：

那么在N支樣品容積為v的發(fā)酵管試驗中，恰好出現r支顯陰性反應，N-r支顯陽(yáng)性反應的概率為：

在N₁支樣品容積v₁、N₂支樣品容積v₂、N₃支樣品容積v₃毫升的發(fā)酵管試驗中，如果呈陰性反應的支數恰好分別是r₁、r₂及r₃，而呈陽(yáng)性反應的支數恰好分別為N₁-r₁、N₂-r₂、N₃-r₃時(shí)，每毫升水樣中的大腸菌數仍用λ表示，那么，這一試驗結果發(fā)生的概率為：

好了，公式終于推出來(lái)了。我們的最大可能數就是上面這個(gè)公式中f(λ)最大值時(shí)對應的λ值，也就是我們想知道的濃度值。

先介紹一個(gè)最原始的計算過(guò)程。

這個(gè)公式中現在有四個(gè)未知量，N、r、v和λ。如果帶入具體試驗，你會(huì )發(fā)現其實(shí)只有一個(gè)λ是真正未知的。

例如，我們做9管法，稀釋度選10倍、100倍和1000倍，陽(yáng)性管數是1-0-0（本來(lái)想算3-2-1，結果嘔血三升，實(shí)在算不下去，放棄了，又選了一個(gè)簡(jiǎn)單的）那通過(guò)查MPN表結果是3.6MPN/g。那么N₁、N₂、N₃都是3，r₁、r₂、r₃代表陰性管，所以分別是2、3、3。那么v1、v2、v3就是稀釋度下樣品含量分別是0.1mL、0.01mL和0.001mL。未知的就只剩λ了，那么把上面這些參數代入公式，計算如下：

把這個(gè)公式轉化成函數圖是這樣的：

是不是和拋硬幣的那個(gè)圖完全不同了？這上面橫坐標就是1-0-0中對應的所有可能的菌濃度。我們要找的是最可能的值，也就是函數的最高點(diǎn)對應的λ值。

怎么算呢？用微積分求導數就行了，最高點(diǎn)的導數是等于0的。所以把上述公式求導：

這就是剛才公式的導函數，只要讓這個(gè)導函數等于0，求相應的λ值就行了。具體計算對數學(xué)專(zhuān)業(yè)人士應該挺簡(jiǎn)單的，但是對我們還是挺復雜的，所以我們再取個(gè)巧，直接做函數圖，圖上會(huì )幫我們計算。

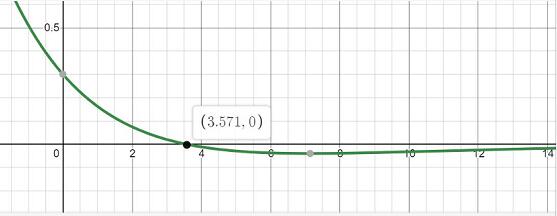
看結果出來(lái)了，是3.571，四舍五入之后就是MPN表上的3.6了。我們看到的MPN表上的數值都是四舍五入之后的。

這么計算太麻煩了，所以在1942年，Thomas先生給出了一個(gè)估算MPN值的方法，計算過(guò)程比上面的方法簡(jiǎn)單了很多很多。目前FDA介紹的也是這種估值的算法。注意，這個(gè)方法算出是估值，不是準確值。

公式是這樣的：

帶入公式：

估值是3.59，我們用第一個(gè)方法算出來(lái)的是3.571，結果還是很接近的，但是計算過(guò)程可是省事了很多，既不用求導數也不用解方程。而且兩個(gè)數四舍五入之后都是3.6。

好了，計算方法都介紹完了，如果每次我們做完試驗都需要這么計算一番才知道結果，是不是很痛苦？所以McCrady先生才做了MPN表，表格的每一項都是計算出來(lái)的，繪成表格后使用就方便了。只要查出管數的陽(yáng)性數就可以查到相應的MPN值了。所以請珍惜和重視我們的MPN表吧，每個(gè)數據都是一點(diǎn)點(diǎn)算出來(lái)的，剎費苦心啊。

最后說(shuō)一點(diǎn)，MPN/g與MPN/100g能不能換算？怎么換算呢？看完上面的介紹和計算應該明白了吧。可以換算，直接把MPN/g乘以100，就是MPN/100g。其實(shí)就是公式中λ的單位，現在假設的是個(gè)/mL，分子分母同時(shí)乘以100，就是個(gè)/100mL。

舉個(gè)例子。還是以大腸菌群的國標為例，我們從兩個(gè)標準附錄中的MPN表里隨機挑選幾個(gè)組合，列成下表。左邊是2003年的，右邊是2016年的。

上表可以看出兩個(gè)不同，一個(gè)是黃色標注的稀釋度不同，一個(gè)是綠色標注的結果單位不同。為了更直觀(guān)的看到這個(gè)100倍的差異，我們把稀釋度統一一下。根據國標MPN表中備注，選不同稀釋度時(shí)結果可相應放大或縮小一定倍數，那么表格就變成了這樣。

稀釋度統一后，我們再來(lái)看結果，發(fā)現是不是就是100倍的差別？有兩個(gè)不同的，你想到了什么？是不是四舍五入？之前我就提過(guò)，MPN表有四舍五入修約的，不同時(shí)代的MPN表保留有效數字的位數不同，所以就修約成了不同的樣子，但是他們本質(zhì)上就是原始公式中λ的單位而已。

如果看到這里，在不翻書(shū)不求助的情況下，上面的計算你都能看懂。

恭喜您了，您一定是萬(wàn)中無(wú)一的數學(xué)人才?。。。?！

畢竟大學(xué)畢業(yè)也好幾年了，就算剛畢業(yè)，也距離大一大二好幾年了。很多東西都還給老師了，您如果還能記得，請一定重視自己的數學(xué)天賦，您的未來(lái)不可限量?。。。?！??